ELECTRODINAMICA Y ELECTROCINETICA
Justificación del término
Cuando los campos eléctrico y magnético varían "lentamente", es decir, puede estudiarse el movimiento de las partícula cargadas en esos campos mediante las aproximaciones
electrostática y
magnetostática.
Aquí "lentamente" siginifica que durante cualquier intervalo de tiempo
de duración aproximada d/c (siendo d la máxima distancia entre las
cargas intervinientes y c la
velocidad de la luz).
El hecho de que la electrostática y la magnetostática sean sólo
aproximaciones válidas para distancias pequeñas y variaciones lentas,
hace que las descripciones de mediados del
siglo XIX acerca de campos variables, tales como la
Ley de Faraday y la
Ley de Biot-Savart son inexactas. En la práctica, esto implica el estudio de la
radiación electromagnética.
La electrodinámica es la forma más avanzada del
electromagnetismo clásico. Muchos de los resultados de la electrodinámica han sido debidos a intentos de explicar leyes
ópticas como la
Ley de Snell mediante el uso de versiones apropiadamente simplificadas de las
ecuaciones de Maxwell, o bien de explicar fenómenos como la dispersión y absorción de la luz.
[
editar] Electrodinámica clásica
Albert Einstein desarrolló la
relatividad especial
merced a un análisis de la electrodinámica. Durante finales del siglo
XIX los físicos se percataron de una contradicción entre las leyes
aceptadas de la electrodinámica y la
mecánica clásica. En particular, las ecuaciones de Maxwell predecían resultados no intuitivos como que la
velocidad de la luz es la misma para cualquier observador y que no obedece a la
invariancia de Galileo.
Se creía, pues, que las ecuaciones de Maxwell no eran correctas y que
las verdaderas ecuaciones del electromagnetismo contenían un término que
se correspondería con la influencia del
éter lumínico.
Después
de que los experimentos no arrojasen ninguna evidencia sobre la
existencia del éter, Einstein propuso la revolucionaria idea de que las
ecuaciones de la electrodinámica cuántica eran correctas y que las
ecuaciones de la mecánica clásica eran inexactas, lo que le llevó a la
formulación de la
relatividad especial. [
editar] Historia y predicciones
La
QED es una de las teorías más precisas de cuantas se crearon en el
siglo XX. Es capaz de hacer predicciones de ciertas magnitudes físicas
con hasta veinte cifras decimales de precisión, un resultado poco
frecuente en las teorías físicas anteriores. Por esa razón la teoría fue
llamada "la joya de la física". Entre sus predicciones más exactas
están:
El
momento magnético anómalo del
electrón y del
muón,
para el cual la ecuación de Dirac predecía un valor de exactamente el
doble del valor clásico. Para el electrón la QED predica un valor:
Donde:
es la
carga eléctrica del electrón.
es la
constante de Planck.
es la
velocidad de la luz en el vacío.
es la
permitividad eléctrica del vacío.
El valor del
salto de Lamb en los
niveles energéticos del
átomo de hidrógeno.
Shin'ichirō Tomonaga,
Julian Schwinger y
Richard Feynman recibieron los
premios Nobel de Física de
1965 por su desarrollo, sus contribuciones que implicaban una prescripción
covariante y
gauge invariante
para el cálculo de cantidades observables. La técnica matemática de
Feynman, basada en sus diagramas, parecía inicialmente muy diferente del
enfoque teórico de campos, basado en operadores de Schwinger y
Tomonaga, pero fue más adelante demostrado como equivalente. El
procedimiento de
renormalización
para dar sentido a algunas de las predicciones infinitas de la teoría
cuántica del campo también encontró su primera puesta en práctica
acertada en electrodinámica cuántica.
[
editar] Descripción de la teoría
Matemáticamente, QED tiene la estructura de una
teoría de gauge abeliana con U(1) el
grupo de gauge. El
campo de gauge que media la interacción entre
campos de spin-1/2 con carga es el
campo electromagnético.
Físicamente, esto se traduce al marco de partículas cargadas (y de su
antipartículas) que interactúan por el intercambio de
fotones. Estas interacciones se pueden describir pictóricamente con
diagramas de Feynman, y QED fue históricamente la teoría a la cual los diagramas de Feynman se aplicaron primero.
QED
fue la primer teoría cuántica del campo en la cual las dificultades
para construir una descripción completa de campos y de creación y
aniquilación de partículas cuánticas, fueron resueltas
satisfactoriamente.
[
editar] Formulación matemática
El
lagrangiano de QED para la interacción del
electrón y el
positrón a través del
fotón s es
y su
adjunto de Dirac
son los campos que representan partículas de carga eléctrica,
específicamente el electrón y los campos del positrón representados como
espinor de Dirac.
La parte del lagrangiano conteniendo el
tensor de
campo electromagnético describe la evolución libre del
campo electromagnético, mientras que la
ecuación de Dirac con la
derivada covariante de
gauge describe la evolución libre de los campos del
electrón y del
positrón así como su interacción con el
campo electromagnético.CORRIENTE ELECTRICA.
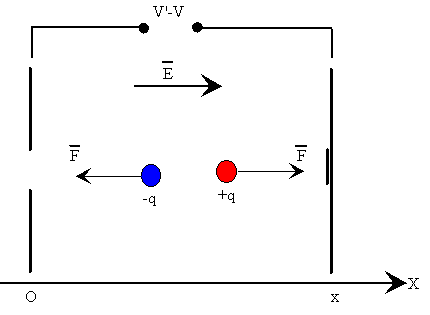
Se
ha dicho que las cargas eléctricas pueden moverse a través de
diferencias de potencial. Naturalmente, deberán de hacerlo por medio de
los conductores (excepto en el caso especial de las válvulas de vacio,
pero también éstas están terminadas en conductores).
A este
movimiento de cargas se le denomina corriente eléctrica. La causa que
origina la corriente eléctrica es la diferencia de potencial. Las cargas
"caen" del potencial más alto al más bajo. Las únicas partículas que
pueden desplazarse a lo largo de los conductores, debido a su pequeño
tamaño, son los electrones, que como se sabe, son cargas de signo
negativo. Entonces, la corriente eléctrica se mueve desde el potencial
negativo, que es la fuente de electrones, hacia el positivo, que atrae
las cargas negativas. Esta circulación recibe el nombre de CORRIENTE
ELECTRONICA, para distinguirla de la CORRIENTE ELECTRICA, que fluye al
revés, de positivo a negativo. Este último acuerdo fué tomado en los
principios de la electricidad, por considerar que las cargas "caen" del
potencial más alto al más bajo, cuando se creía que eran las cargas
positivas las que se desplazaban. En la actualidad, coexisten ambos
criterios, uno real y otro ficticio. A la hora de resolver circuitos
puede aplicarse uno u otro, ya que, tratándose de convenios, ambos dan
el mismo resultado.
Es evidente que no en cualquier circunstancia,
circulará el mismo número de electrones. Este depende de la diferencia
de potencial y de la conductividad del medio. Una forma de medir el
mayor o menor flujo de cargas es por medio de la INTENSIDAD DE CORRIENTE
(o también, simplemente, CORRIENTE), que se define como la cantidad de
carga que circula por un conductor en la unidad de tiempo (un segundo).
Según esto:
I = Q / t ó Q = I x t
La intensidad de corriente eléctrica se expresa en AMPERIOS que, por definición, es el número de culombios por segundo.
Los
divisores más usuales del amperio son: El miliamperio (mA) que es la
milésima parte del amperio, por lo que: 1 A. = 1.000 mA. El
microamperio (mA) que es la millonésima parte del amperio, por lo que: 1
A. = 1.000.000 mA
Amperios A
Miliamperios mA
Microamperios mA
1 Amperio =
1
103
106
1 Miliamperio =
10-3
1
103
1 Microamperio =
10-6LEY DE OHM
Debe
existir alguna relación entre la diferencia de potencial aplicada en
los extremos de un conductor y la corriente que atraviesa ese conductor.
Ohm encontró experimentalmete que esta relación era proporcional, es
decir, que para un conductor dado, cuando, por ejemplo, se duplica o se
triplica la diferencia de potencial, se duplica o se triplica la
coriente, respectivamente.
Dicho de otro modo, cuando una corriente
eléctrica atraviesa un conductor, cra en éste una diferencia de
potencial directamente proporcional a la corriente. A esta constante de
proporcionalidad se le llama resistencia. La mayor o menor resistencia
de un conductor es la mayor o menor dificultad que opone al paso de la
corriente. Y así tendremos buenos y malos conductores de la corriente en
función de que tengan pequeña o alta resistencia respectivamente.
Obviamente, los aislantes ( no conducen la corriente) tendrán una
resistencia altísima.
Si se representa la resistencia del conductor
por la letra R, la diferencia de potencial en los extremos del
conductor por la letra V, y la corriente que circula por él, con la
letra I la ley de Ohm puede formularse como:
V= I x R
que es lo mismo que decir I = V / R ó R = V / I
La unidad de resistencia eléctrica es el OHMIO, simbolizado por la letra griega W (omega)
Los
múltiplos más usuales del Ohmio son: El Kilohmio que es igual a 1.000
Ohmios => 1KW = 1.000 W El Megaohmio ques es igual a 1.000.000
Ohmios => 1MW = 1.000.000 W
En el lenguaje normal, muchas veces
se abrevian estos nombres y, en vez de decir Kilohmio, se dice
sencillamente K o, en vez de decir Megaohmio, sencillamente Mega. o M.
La
resistencia de un conductor depende de sus dimensiones: es decir,
tendrá más resistencia cuanto más estrecho y largo sea dicho conductor.
Esto resulta intuitivo si se considera la resistencia como la dificultad
que opone al paso de la corriente.
Dicha proporcionalidad se expresa como: R = r x l / S
Donde:
R es la resistencia medida en ohmios l es la longitud medida en
metros. S es la sección (área) transversal del conductor, en metros
cuadrados. r es una constante que depende del material con que está
fabricado el conductor y se llama RESISTIVIDAD o RESISTENCIA ESPECIFICA
del material en cuestión, y que da la resistencia por cada unidad de
longitud y de sección.
(Ver Tabla de resistividades) A veces se utiliza el inverso de la RESISTIVIDAD, al que se le llama CONDUCTIVIDAD (s )
s = 1 / r r = 1 / s
representación gráfica de la ley de Ohm
Toda
ley matemática puede representarse gráficamente por medio de un sistema
de ejes coordenados; en el eje horizontal ( llamado eje de abscisas o
eje de las X) se representan los valores de una variable y en el eje
vertical ( eje de ordenadas o eje de las Y) se representan los valores
de la función que correspondan a los dados de la variable. De este modo
se puede ver por medio de la gráfica el comportamiento de esa ley,
resultando ser un método rápido y sencillo, por lo que será profusamente
usado en Electrónica.
V(V)
25
20
15
10
5
0
DV=8V
DI=1A
0
0,5 1 1,5 2 2,5 3 I (A)
Representación
gráficaSupóngase una determinada resistencia por la que se hacen
circular distintas corrientes, produciéndose sendas caídas de potencial,
según la tabla:
Para 0,5 A....................... 4 V. Para 1
A....................... 8 V. Para 2 A....................... 16
V. Para 3 A....................... 24 V.
Una vez determinada la
unidad de longitud en cada eje, (en el eje del voltaje V se han tomado
de 5 en 5 voltios, y en el eje de la corriente I de 0,5 en 0,5 amperios)
se procederá a tomar sobre ellos los valores de la tabla.
Cada
pareja define un punto: el valor de 0,5 en el eje horizontal corresponde
4 en el eje vertical, y a 1 en el horizontal corresponde 8 en el
vertical, y así sucesivamente.
La línea que pasa por los puntos así
formados (ver figura) es la representación gráfica de la función. En
este caso (Ley de Ohm), resulta ser una recta, y diremos que esta ley es
LINEAL.
Una vez dibujada la función, en nuestro caso la recta, se puden obtener de ella nuevos valores.
Por ejemplo, ¿ qué caida de potencial se produce para una corriente de 2,5 A. ?
Respuesta (viendo la figura): 20 V. ¿ Qué corriente circula cuando la d.d.p. (diferencia de potencial) es de 10 V. ?
Respuesta (viendo la figura ): 1,25 A. ¿ Cuánto vale la resistencia ?
Respuesta: R = DV / DI
Viendo la figura DV = 8 V DI = 1 A.
R = 8 / 1
R = 8 W
y ese valor lo obtendremos para cualquier DV que elijamos de la figura
Volver a lecciones Volver a electrodinámica ALBERGUES / HOSTELS VALENCIA RESISTORES (También llamados RESISTENCIAS)
Los
circuitos electrónicos necesitan incorporar resistencias. Es por esto
que se fabrican un tipo de componentes llamados resistores cuyo único
objeto es proporcionar en un pequeño tamaño una determinada resistencia,
especificada por el fabricante. El símbolo de un resistor es: ó
Hay resistencias de varios tipos. Los tipos más usuales son:
BOBINADAS: Sobre una base de aislante en forma de cilindro se
arrolla un hilo de alta resistividad (wolframio, manganina, constantán).
La longitud y sección del hilo, asi como el material de que está
compuesto, darán una resistencia. Esta suele venir expresada por un
número impreso en su superficie. Se utilizan para grandes potencias,
pero tienen el inconveniente de ser inductivas. AGLOMERADAS: Una pasta
hecha con gránulos de grafito (el grafito es una variedad del carbono
puro; la otra es el diamante). El valor viene expresado por medio de
anillos de colores, con un determinado código. DE PELICULA DE CARBON:
Sobre un cilindro de cerámica se deposita una fina película de pasta de
grafito. El grosor de ésta, y su composición, determinan el valor de la
resistencia. PIROLITICAS: Similares a las anteriores, pero con la
película de carbón rayada en forma de hélice para ajustar el valor de la
resistencia. Son inductivas.
3.4 RESISTORES VARIABLES
Hay
veces en que interesa disponer de una resistencia cuyo valor pueda
variarse a voluntad. Son los llamados reostatos o potenciómetros. Se
fabrican bobinados o de grafito, deslizantes o giratorios. Se suelen
llamar potenciómetros cuando poseen un eje practicable, y resistencias
ajustables cuando para vararlas se precisa la ayuda de una herramienta,
porque una vez ajustados no se van a volver a retocar más.
Los potenciómetros se representan en los circuitos por :
3.5 RESISTORES ESPECIALES
Existen
resistores fabricados con materiales especiales, comúnmente
semiconductores, cuya resistencia no es constante, sino que depende de
algún parámetro exterior. Por ejemplo:
LDR
LDR (Litgh Dependent Resistance) Resistencia dependiente de la luz
VDR
VDR (Voltage Dependent Resistance) Resistencia dependiente del Voltaje
PTC
PTC (Positive Temperature Coefficient) Coeficiente de Temperatura Positivo
NTC
NTC ( Negative Temperature Coefficient) Coeficiente de Temperatura Negativo
3.6 LIMITACIONES DE LOS RESISTORES
A
la hora de escoger un resistor hay que tener en cuenta, además de su
valor óhmico, otros parámetros, tales como la máxima potencia que es
capaz de disipar y la tolerancia.
Respecto a la primera, es preciso
considerar que una resistencia se calienta al paso por ella de una
corriente (como se verá más adelante). Debido a esto, hace falta
dimensionar el resistor de acuerdo con la potencia calorífica que vaya a
disipar en su funcionamiento normal. Se fabrican resistores de varias
potencias nominales, y se diferencian por su distinto tamaño.
La
tolerancia es un parámetro que expresa el error máximo sobre el valor
óhmico nominal con que ha sido fabricado un determinado resistor. Por
ejemplo, un resistor de valor nominal 470 W con una tolerancia del 5 %
quiere decir que el valor óhmico real de ese resistor puede oscilar
entre el valor nominal más el 5 % del mismo, y el valor nominal menos el
5 %. Es decir, entre :
470 - 0,05 x 470 = 446,5 470 + 0,05 x 470 = 493,5
Si
no se usan siempre resistores de alta precisión (baja tolerancia) es
porque el coste es elevado y para las aplicaciones normales es
suficiente con una tolerancia relativamente alta.
3.7 VALORES COMERCIALES
No
se fabrican resistores de todos los valores posibles por razones obvias
de economía. Además sería absurdo, ya que, por ejemplo, en un resistor
de 100 W y 10 % de tolerancia, el fabricante nos garantiza que su valor
está comprendido entre 90 W y 100 W , por lo tanto no tiene objeto
alguno fabricar resistores de vaolres comprendidos entre estos dos
últimos.
Hay tolerancias del 1 por mil, del 1 %, 5 %, 10 % y 20 %.
Para
la serie de resistores que se fabrican con una tolerancia del 10 % que
es la más utilizada, los valores comerciales son: 10 18 33 56 12
22 39 68 15 27 47 82
y los mismos seguidos de ceros.
Resistores
de valores muy pequeños no son comunes, por la dificultad que entraña
ajustar su valor. Resistores de valores muy grandes son difíciles de
conseguir, porque en ellos comienza a tener importancia fenómenos como
la resistencia superficial, condiciones ambientales, étc. y tampoco es
normal su uso.
Por ejemplo:
En la serie de resistores con
tolerancia del 10 % el valor más pequeño es de 4,7 W y el mayor de 22 MW
. En la serie del 5 % los valores extremos son 0,33 W 7 10 MW .
3.8 CONDUCTANCIA
La
conductancia es una magnitud eléctrica que se define como la inversa de
la resistencia y se representa con la letra G. Por analogía con la
resistencia, podría decirse que la conductancia es la facilidad que un
conductor ofrece al paso de la corriente a través de él.
G = 1 / R ó R = 1 / G
La unidad de conductancia es el MHO (inverso de Ohm), y se representa por la letra omega invertida.
3.9 CODIGO DE COLORES
Ya
se ha dicho que los valores óhmicos de los resistores se suelen
representar por medio de unos anillos de color pintados en el cuerpo de
los mismos. Suelen ser en número de cuatro, y su significado es el
siguiente:
1er. anillo : 1ª cifra 2º. anillo : 2ª cifra 3er.
anillo : Número de ceros que siguen a los anteriores. 4º. anillo :
Tolerancia
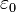 es 8,8541878176x10-12 F/m.
es 8,8541878176x10-12 F/m.

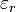 (también llamada
(también llamada 
 es la
es la  (
(